Emitteriga stabiliseeritud BJT eelarveahel

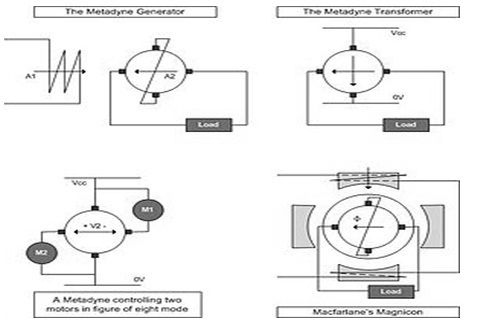
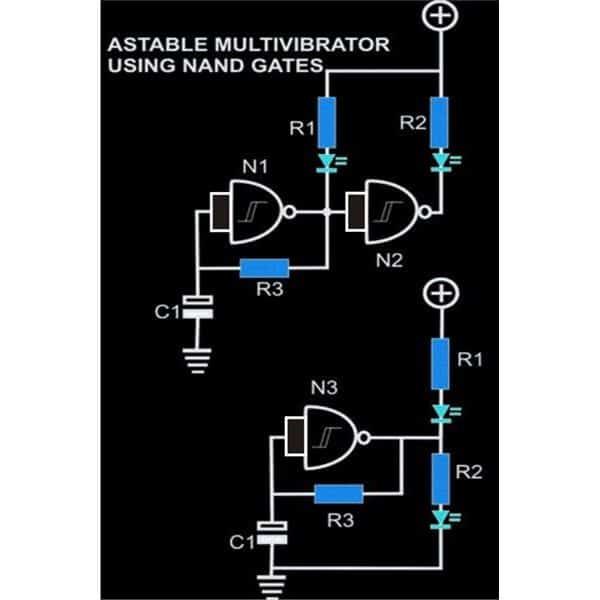
Konfiguratsiooni, milles bipolaarse ristmiktransistori või BJT-d tugevdatakse emitteri takistiga, et suurendada selle stabiilsust ümbritseva õhu temperatuuri muutumise suhtes, nimetatakse BJT emitteri stabiliseeritud eelpinge vooluringiks.

Oleme juba uurinud, mis on Alalisvoolu kallutamine transistorides , nüüd liigume edasi ja õpime, kuidas emitteritakisti saab kasutada BJT alalisvoolu eelarvevõrgu stabiilsuse parandamiseks.

Emitteri stabiliseeritud eelarveahela rakendamine

Emitteri takisti lisamine BJT alalisvoolu eelarvele tagab ülima stabiilsuse, see tähendab, et alalisvoolu eelpingevoolud ja -pinged on jätkuvalt lähedasemad sellele, kuhu vooluahel on fikseerinud, arvestades väliseid parameetreid, näiteks temperatuuri kõikumisi, ja transistori beeta (võimendus),

Allpool toodud joonisel on kujutatud transistori alalisvoolu eelpingevõrk, millel on emitteritakisti emitteriga stabiliseeritud eelpinge rakendamiseks BJT olemasoleva fikseeritud eelhäälestuse konfiguratsioonis.

Joonis 4.17 BJT eelpinge ahel emitteri takistiga

Aruteludes alustame disaini analüüsi, kontrollides kõigepealt vooluahela baas-emitteri piirkonna ümber asuvat silmust ja seejärel kasutage tulemusi ahela kollektori-emitteri külje ümber asuva silmuse edasiseks uurimiseks.

Baas-emitteri silmus

Võime ülaltoodud baas-emitteri silmuse joonistada joonisel 4.18 allpool näidatud viisil ja kui seda rakendame Kirchhoffi pingeseadus sellel silmusel päripäeva aitab meil saada järgmise võrrandi:

+ Vcc = IBRB - VBE - IERE = 0 ------- (4.15)

Meie eelmistest aruteludest teame, et: IE = (β + 1) B ------- (4.16)

IE väärtuse asendamine ekvivalendis (4.15) annab järgmise tulemuse:

Vcc = IBRB - VBE - (β + 1) IBRE = 0

Terminite vastavasse rühma viimine annab järgmise tulemuse:

Kui tuletate meelde meie eelmisi peatükke, tuletati fikseeritud eelarvevõrrand järgmisel kujul:

Kui võrrelda seda fikseeritud eelarvevõrrandit (4.17) võrrandiga, leiame, et praeguse IB kahe võrrandi ainus erinevus on termin (β + 1) RE.

Kui võrrandit 4.17 kasutatakse seeriapõhise konfiguratsiooni joonistamiseks, suudame välja tuua huvitava tulemuse, mis tegelikult sarnaneb võrrandiga 4.17.

Võtke joonisel 4.19 järgmise võrgu näide:

Kui lahendame praeguse IB süsteemi, saadakse sama võrrand, mis on saadud ekvivalendis. 4.17. Pange tähele, et peale pinge alusest emitterini VBE võib takisti RE näha uuesti ilmuvat baasahela sisendis taseme võrra (β + 1).

See tähendab, et emitteri takisti, mis moodustab osa kollektori-emitteri silmusest, kuvatakse kui (β + 1) RE aluse-emitteri silmuses.

Eeldades, et enamiku BJT-de korral võib β olla enamasti üle 50, võib transistoride emitteri takisti olla aluse ahelas oluliselt suurem. Seega oleme võimelised tuletama joonisele fig.4.20 järgmise üldise võrrandi:

Ri = (β + 1) RE ------ (4.18)

See võrrand on paljude tulevaste võrkude lahendamisel üsna mugav. Tegelikult hõlbustab see võrrand võrrandi 4.17 meeldejätmist lihtsamal viisil.

Ohmi seaduse järgi teame, et võrgu kaudu toimuv vool on pinge jagatud vooluahela takistusega.
Baas-emitteri disaini pinge on = Vcc - VBE

Punktis 4.17 nähtud takistused on RB + RE , mis kajastub kui (β + 1), ja tulemus on see, mis meil on võrrandis 4.17.

Koguja – Emitteri aas

Ülaltoodud joonisel on näidatud kollektori ja emitteri silmus, rakendades Kirchhoffi seadus näidatud silmusele päripäeva, saame järgmise võrrandi:

+ Eile + SA OLED + ICRC - VCC = 0

Emiteri stabiliseeritud eelarveahela praktilise näite lahendamine, nagu allpool esitatud:



Eeltoodud joonisel 4.22 toodud emitteri eelarvevõrgu puhul hinnake järgmist:

1. IB
2. IC
3. SA OLED
4. U
5. JA
6. JNE
7. VBC

Küllastuse taseme määramine

Maksimaalne kollektori vool, mis muutub kollektoriks küllastustase emitteri eelarvamuste võrgu arvutamiseks kasutati sama strateegiat, mida oli rakendatud meie varem fikseeritud eelarveahel .

Seda saab rakendada, tekitades lühise üle BJT kollektori ja emitteri juhtmete, nagu on näidatud ülaltoodud diagrammil 4.23, ja seejärel saame hinnata saadud kollektori voolu järgmise valemi abil:

Näiteprobleem küllastusvoolu lahendamiseks emitteriga stabiliseeritud BJT-ahelas:

Koormusjoone analüüs

Emitter-bias BJT vooluringi koormusjoone analüüs on üsna sarnane meie varem käsitletud fikseeritud eelarvamusega konfiguratsiooniga.

Ainus erinevus on IB tase [tuletatud meie ekv. (4.17)] määratleb IB taseme omadustel, nagu on näidatud järgmisel joonisel 4.24 (tähistatud kui IBQ).